重积分

二重积分

性质：

1. $\iint _D[f(x,y) \pm g(x,y)]dxdy=\int \int _Df(x,y)dxdy+\int \int _Dg(x,y)dxdy$

2. $\int \int _Dkf(x,y)dxdy=k\int \int _Df(x,y)dxdy$

3. $D=D_1+D_2 \Rightarrow \int \int _{D_1}f(x,y)dxdy+\int \int _{D_2}f(x,y)dxdy$

4. $\int \int _Ddxdy=A,A$为$D$的面积

5. 在$D$上有$f(x,y)\leq g(x,y)$则$\int \int _Df(x,y)dxdy \leq \int \int _Dg(x,y)dxdy$,若$f(x)$不恒等于$g(x)$,则 $\int \int _Df(x,y)dxdy < \int \int _Dg(x,y)dxdy$

6. 对称性质：

   • 关于$x$轴对称时，一侧区域为$D_1$:

\[\begin{cases} f(x,-y)=-f(x,y),\int \int _Df(x,y)dxdy=0\\ f(x,-y)=f(x,y),\int \int _Df(x,y)dxdy=2\int \int _{D_1}f(x,y)dxdy \end{cases}\]

• 关于$y$轴对称类似

• 关于$y=x$对称：$\int \int _Df(x,y)dxdy=\int \int _Df(y,x)dxdy$

• 关于$y=-x$对称：$\int \int _Df(x,y)dxdy=\int \int _Df(-y,-x)dxdy$

1. 中值定理： 设$f(x,y)$在$D$上连续，$A$为$D$面积，则一定存在$(m,n) \in D$使$\int \int _D f(x,y)dxdy=f(m,n)A$

计算方法：

1. 直角坐标法

   \[\int \int _Df(x,y)d\alpha=\int^b_adx\int^{\phi _2(x)}_{\phi _1(x)}f(x,y)dy\]

   注意：以下情况积不了要改变积分次序

   \[\begin{cases} x^{2n}e^{\pm x^2}dx\\ e^{\frac{k}{x}}dx\\ cos\frac{k}{x}dx\\ sin \frac{k}{x}dx \end{cases}\]

   8.1例题：$\int ^1_0dy\int_y^1 e^{x^2}dx$

   答案

2. 极坐标法（一般$D$或$f(x,y)$中包含$x^2+y^2$使用极坐标法） 令$x=rcos\theta,y=rsin\theta,\rightarrow d\alpha=rdrd\theta$

   8.2例题$D:x^2+y^2\leq2x,$求$\int \int_D x^2+xy d\alpha$

   答案

三重积分

性质：

1. $\int \int \int _{\Omega}1dv=v$
2. 对称性与二重积分基本一样

计算方法：

1. 铅直投影法：

\[\iiint _{\Omega}f(x,y,z)dv=\int \int _{D_{xy}}dxdy\int^{\phi_2(x,y)}_{\phi_1(x,y)}f(x,y,z)dz\]

1. 切片法：

   \[\int \int \int _{\Omega}f(x,y,z)dv=\int ^c_ddz\int \int _{D_z}f(x,y,z)dxdy\]

   8.3例题：$I=\int\int\int_{\Omega}\sqrt{x^2+y^2}dv,x^2+y^2+z^2\leq4$

   答案

2. 球面坐标变化法 见图变换：

   
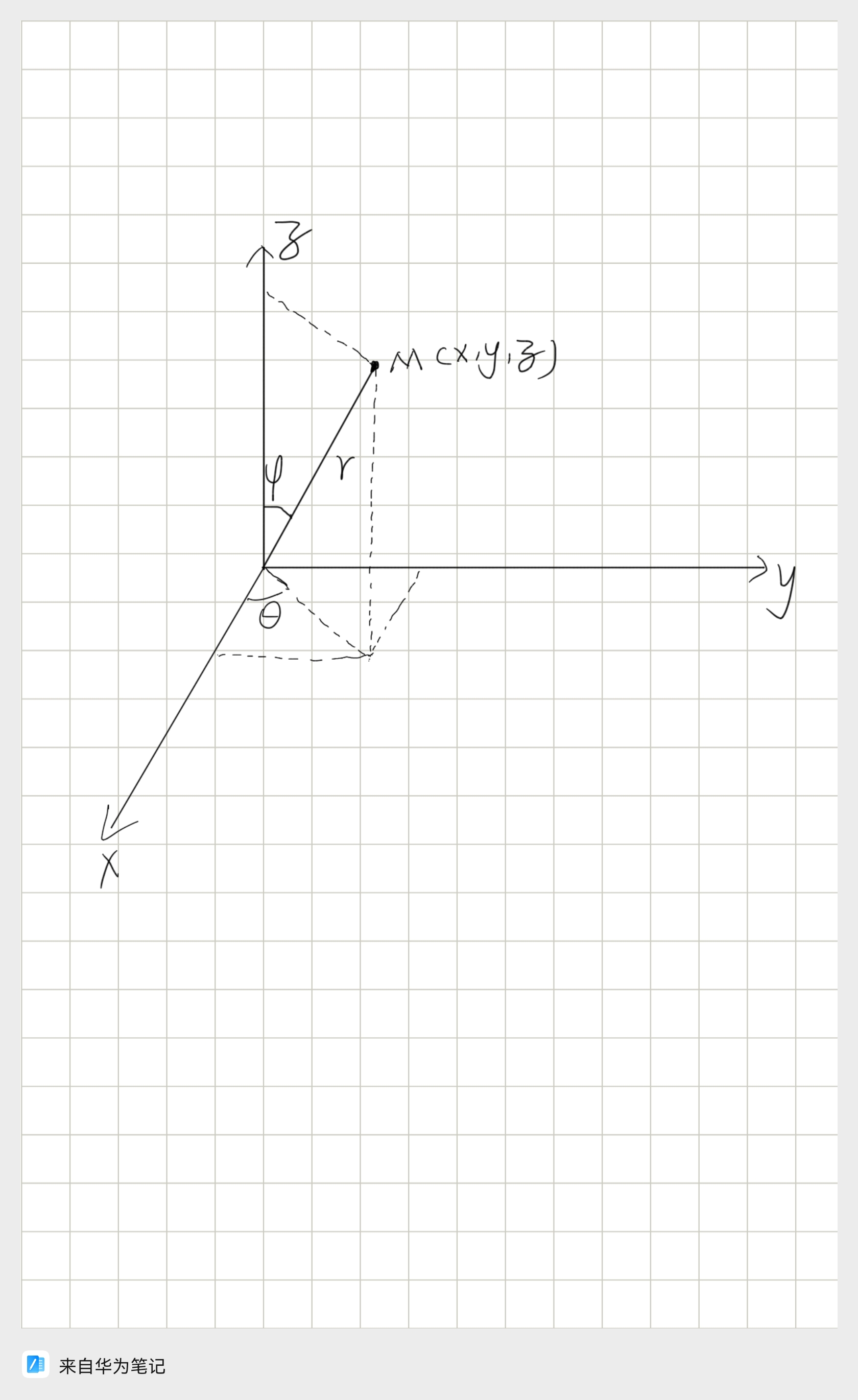   说明
   \[\begin{cases} x=rsin\phi cos\theta\\ y=rsin\phi sin\theta\\ z=rcos\phi\\ dxdydz=r^2sin\phi drd\theta d\phi \end{cases}\]

   8.4例题：$I=\int \int \int _{\Omega}zdv,\Omega:x^2+y^2+(z-2)^2 \leq 4$

   答案