第五章:定积分及其应用
§1 定义
设 $f(x)$ 在 $[a,b]$ 上有界,$\lambda = max${$\xi_1,\xi_2,…,\xi_n$},则 $\lim_{\lambda \to 0}f(\xi _i)\Delta \xi_i$ 为 $f(x)$ 在 $[a,b]$ 上的积分。
§2 定积分一般性质
-
$\int^a_af(x)dx=0$
-
$\int^b_af(x)dx=-\int^a_bf(x)dx$
-
$\int^b_af(x)+g(x)dx=\int^b_af(x)dx+\int^b_ag(x)dx$
-
$\int^b_amf(x)dx=m\int^b_af(x)dx$
-
$\int^c_af(x)dx=\int^b_af(x)dx+\int^c_bf(x)dx$
-
几何性质
\[\begin{cases} f(x)\geq 0,\int^b_af(x)dx=s\\ f(x)\leq 0,\int^b_af(x)dx=-s \end{cases}\]$f(x)$ 有正有负的时候 $\int^b_af(x)dx=s_正-s_负$
-
$f(x),g(x)$ 在 $[a,b]$ 可积,且 $f(x)>g(x)$ ,则 $\int^b_af(x)dx>\int^b_ag(x)dx$
-
$f(x),\lvert f(x)\rvert$ 在 $[a,b]$ 可积$\rightarrow \lvert\int^b_af(x)dx\rvert\leq \int^b_a\lvert f(x)\rvert dx$
-
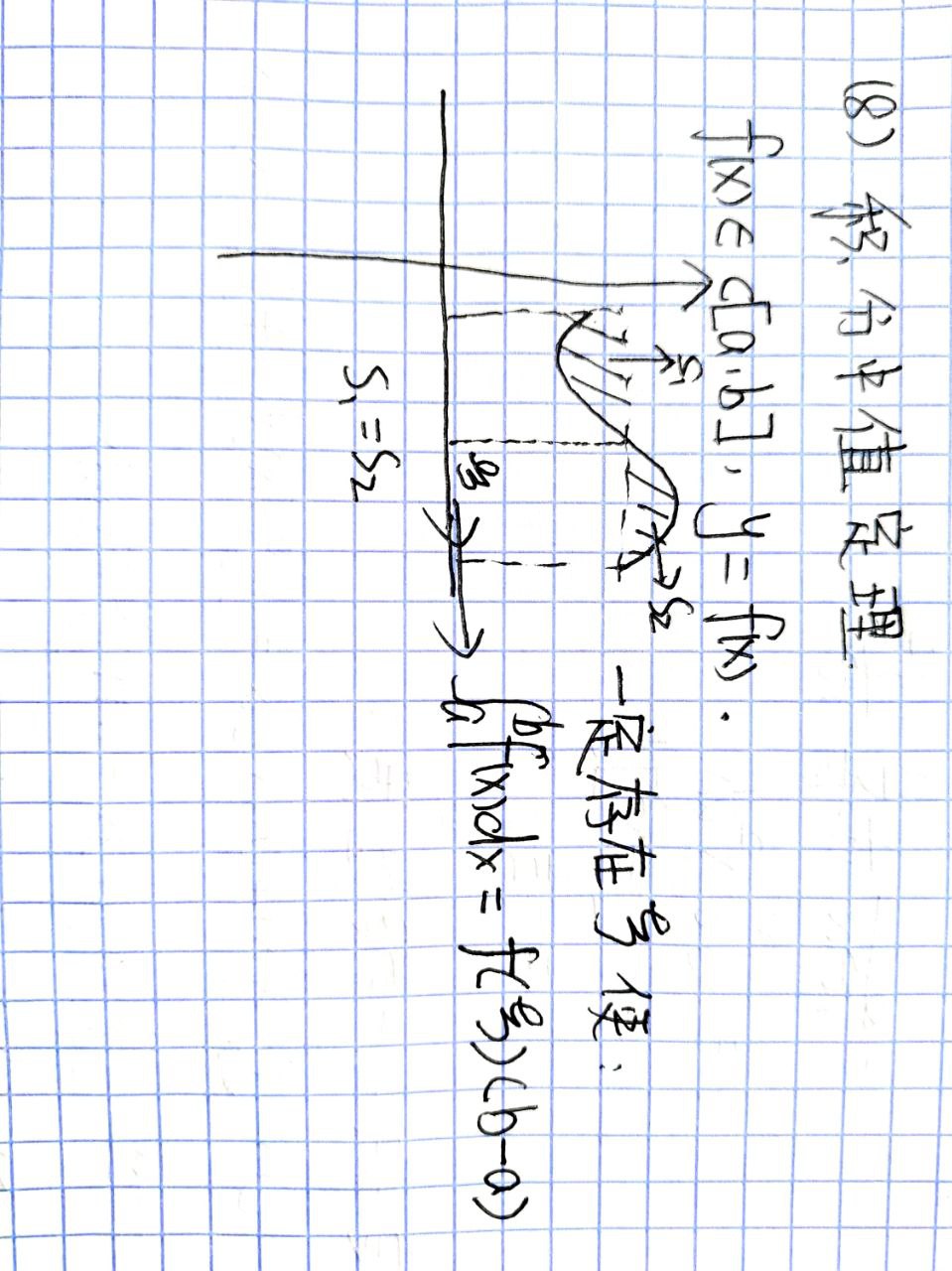
积分中值定理
$f(x) \in [a,b],f(x) $ 在 $[a,b]$ 可积,一定存在$\xi \in [a,b] \rightarrow \int^b_af(x)dx=f(\xi)(b-a)$
 说明
说明
§3 定积分基本定理
-
积分中值定理推论(拉格朗日版)
$f(x) \in [a,b],f(x) $ 在 $[a,b]$ 可积,一定存在$\xi \in (a,b)\rightarrow \int^b_af(x)dx=f(\xi)(b-a)$
例题 $f(x) \in c[0,1],f(x)$在$(0,1)$可导$,f(0)=\int^1_0f(x)dx,$证明:$\exists \xi \in (0,1),f’(\xi)=0$
-
牛顿莱布尼兹定理 $\int^b_af(x)dx=F(b)-F(a)$
§4 定积分特殊性质
-
性质一: $f(x)$ 在 $[0,1]$ 上可积
\[\lim_{n \to \infty}\frac 1 n \displaystyle \sum^n_{i=1}f(\frac {i-1} n)=\lim_{n \to \infty}\frac 1 n \displaystyle \sum^n_{i=1}f(\frac i n)=\int^1_0f(x)dx\]注意$x=\frac i n$,这个只能在分子分母皆齐,分母比分子高一次的情况下使用
例题
\[\lim_{n \to \infty}\frac{1^2+2^2+...+n^2}{n^3}\] -
性质二:
\[\int^a_{-a}f(x)dx=\int^a_0f(x)+f(-x)dx\] -
性质三:
\[\int^{\frac \pi 2}_0f(sinx)dx=\int^{\frac \pi 2}_0f(cosx)dx\]例题
\[\int^1_0\frac 1 {x+\sqrt{1-x^2}}dx\] -
性质四:
\[I_n=\int^{\frac \pi 2}_0sin^nxdx=\int^{\frac \pi 2}_0cos^nxdx\] \[\begin{cases} I_n=\frac{n-1}nI_{n-2}\\ I_0=\frac{\pi}{2}\\ I_1=1 \end{cases}\]例如:$I_4=\frac{3}{4} * \frac{1}{2} * \frac{\pi}{2}$
例题:
\[\int^{\frac{\pi}2}_{-\frac{\pi}2}(\frac{sin^4x}{1+e^x})dx\] -
性质五:
\[\int^{\pi}_0f(sinx)dx=2\int^{\frac{\pi}2}_0f(sinx)dx\] -
性质六:
\[\int^{\pi}_0xf(sinx)dx=\frac{\pi}2\int^{\pi}_0f(sinx)dx\] -
性质七: $f(x)$是以 $T$ 为周期的可积函数,则:
\[\begin{cases} \int^{a+T}_af(x)dx=\int^{T}_0f(x)dx\\ \int^{nT}_0f(x)dx=n\int^{T}_0f(x)dx \end{cases}\]
§5 反常积分
总之做题思路为:1.定义法直接求出来 2.判别法证明出收敛性再计算
常见反常积分值:$\int_o^{+\infty}e^{-x^2}dx=\frac{\sqrt{\pi}}{2}$
积分区域无限型
-
下限无穷型
\[\int^b_{-\infty}f(x)dx=\lim_{a \to -\infty}\int^b_af(x)dx\]敛散性判别法:
-
若存在$\alpha>1,\lim_{x \to -\infty}x^{\alpha}f(x)$存在,则$\int^b_{-\infty}f(x)dx$收敛
-
若存在$\alpha \leq 1,\lim_{x \to -\infty}x^{\alpha}f(x)=k(k\neq0)或\infty$,则$\int^b_{-\infty}f(x)dx$发散
-
-
上限无穷型
\[\int^{+\infty}_af(x)dx=\lim_{b \to +\infty}\int^b_af(x)dx\]敛散性判别法:
- 若存在$\alpha>1,\lim_{x \to +\infty}x^{\alpha}f(x)$存在,则$\int^{+\infty}_{a}f(x)dx$收敛
- 若存在$\alpha \leq 1,\lim_{x \to +\infty}x^{\alpha}f(x)=k(k\neq 0)或\infty$,则$\int^{+\infty}_{a}f(x)dx$发散
-
上下限无穷型
\[\int^{+\infty}_{-\infty}f(x)dx=\int^{a}_{-\infty}f(x)dx+\int^{+\infty}_{a}f(x)dx\]敛散$\Longleftrightarrow$敛散+敛散
-
$\Gamma$函数
- $\Gamma(\alpha)=\int^{+\infty}_0x^{\alpha -1}e^{-x}dx$
例题:求$\int^{+\infty}_0x^2e^{-x^2}dx$
有无穷间断点型
-
$(a,b]$型 总存在$\epsilon>0$使
\[\int^b_{a+\epsilon}f(x)dx=F(b)-F(a+\epsilon)\] \[\lim_{\epsilon \to {0^+}}[F(b)-F(a+\epsilon)]=\int^b_{a}f(x)dx\]定义法
- $\lim_{\epsilon \to {0^+}}[F(b)-F(a+\epsilon)]=A$,则收敛。
- $\lim_{\epsilon \to {0^+}}[F(b)-F(a+\epsilon)]$不存在,则发散
敛散性判别法
- $\exists \alpha<1,\lim_{x \to a^+}(x-a)^{\alpha}f(x)$存在则收敛
- $\exists \alpha \geq 1,\lim_{x \to a^+}(x-a)^{\alpha}f(x)=k(k\neq0)或\infty$则发散
例题:求$\int^{\frac1 2}_0\frac1 {\sqrt{x-x^2}}dx$
-
$[a,b)$型 总存在$\epsilon<0$使
\[\int^{b+\epsilon}_{a}f(x)dx=F(b+\epsilon)-F(a)\] \[\lim_{\epsilon \to {0^-}}[F(b+\epsilon)-F(a)]=\int^b_{a}f(x)dx\]定义法
- $\lim_{\epsilon \to {0^-}}[F(b+\epsilon)-F(a)]=A$,则收敛。
- $\lim_{\epsilon \to {0^-}}[F(b+\epsilon)-F(a)]$不存在,则发散
敛散性判别法
- $\exists \alpha<1,\lim_{x \to a^-}(b-x)^{\alpha}f(x)$存在则收敛
- $\exists \alpha \geq 1,\lim_{x \to a^-}(b-x)^{\alpha}f(x)=k(k\neq0)或\infty$,则发散
-
$[a,c)\cup(c,b]$型
\[\int^{b}_{a}f(x)dx=\int^{c}_{a}f(x)dx+\int^{b}_{c}f(x)dx\]敛散$\Longleftrightarrow$敛散+敛散
例题:
- $\int^2_0\frac{1}{\sqrt{2x-x^2}}dx$
- $\int^{\frac 3 2}_{\frac 1 2}\frac{1}{\sqrt{|x-x^2|}}dx$